Problem
Given head, the head of a linked list, determine if the linked list has a cycle in it.
There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the next pointer. Internally, pos is used to denote the index of the node that tail's next pointer is connected to. Note that pos is not passed as a parameter.
Return true if there is a cycle in the linked list. Otherwise, return false. (link)
Example 1:
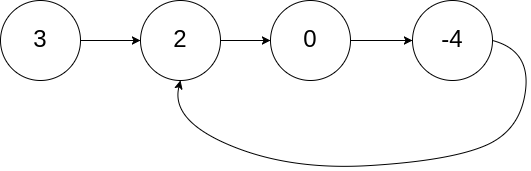
Input: head = [3,2,0,-4], pos = 1
Output: true
Explanation: There is a cycle in the linked list, where the tail connects to the 1st node (0-indexed).
Example 2:
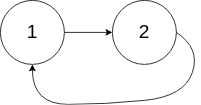
Input: head = [1,2], pos = 0
Output: true
Explanation: There is a cycle in the linked list, where the tail connects to the 0th node.
Example 3:

Input: head = [1], pos = -1
Output: false
Explanation: There is no cycle in the linked list.
Solution
Brute Force Approach
To determine whether a loop exists in the linked list, we utilize a data structure called a set. We iterate through the linked list and store the nodes that are visited. If we encounter a node that is already present in the set, it indicates that a cycle exists.
Time - O(n)
Space - O(n)
public class Solution {
public boolean hasCycle(ListNode head) {
Set<ListNode> set = new HashSet<>();
ListNode temp = head;
while(temp!=null){
if(set.contains(temp)){
return true;
}
set.add(temp);
temp = temp.next;
}
return false;
}
}
Optimal Approach (Tortoise & Hare)
In this method, we employ two pointers: one moving slowly by 1 step and the other moving faster by 2 steps. When these pointers converge on the same node at any given moment, it signifies the presence of a loop.
Proof of the convergence of slow and fast pointers when a loop exists: Continuously calculate the clockwise distance from the fast pointer to the slow pointer. If this distance is denoted as 'd' towards the slow pointer, it consistently diminishes by 1 unit each time, as the fast pointer reduces the distance by 2 while the slow pointer advances by 1. Therefore, the distance between the fast and slow pointers effectively becomes 'd-1'. Consequently, this distance inevitably reduces to 0, indicating that the fast and slow pointers intersect at the same node.
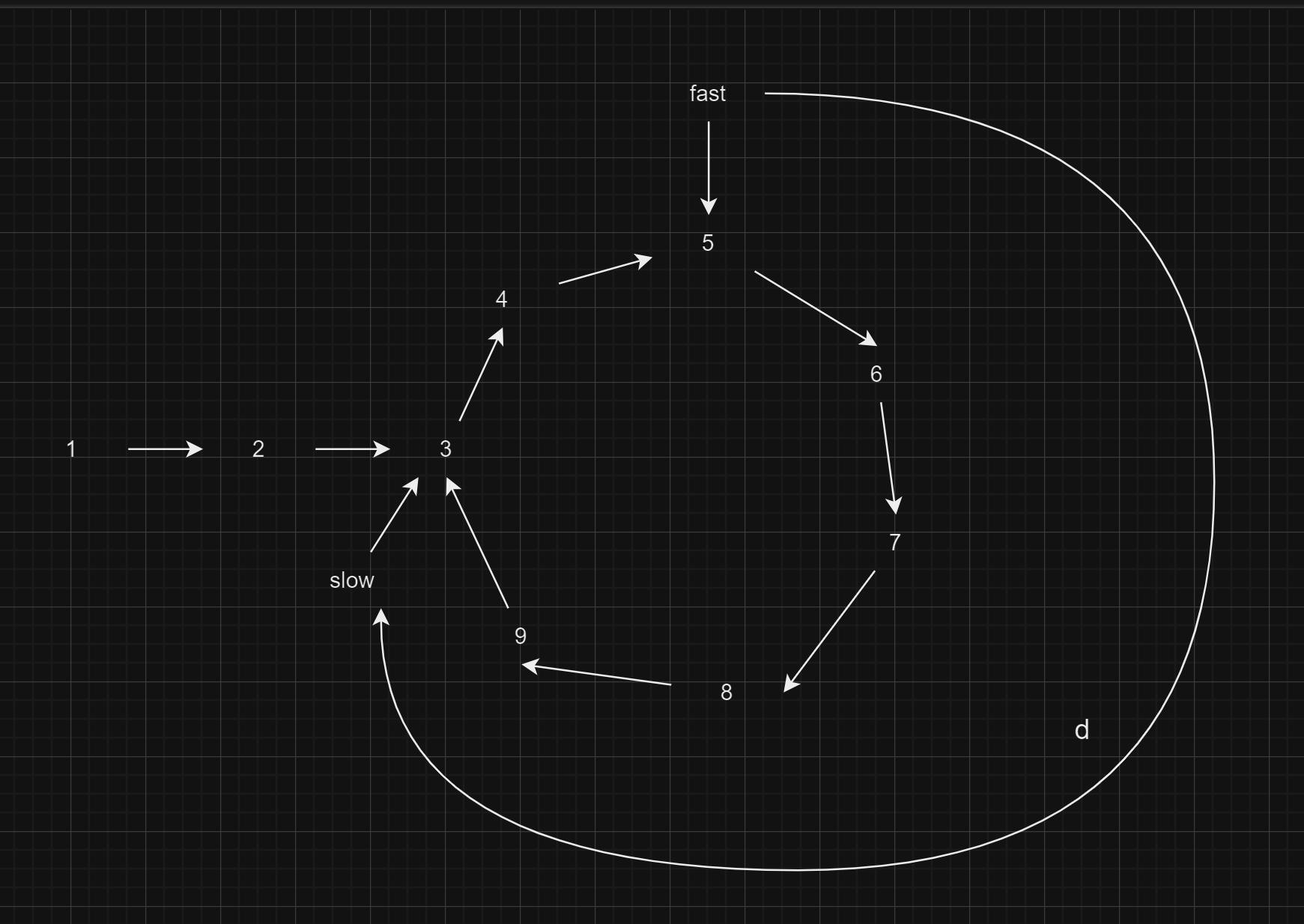
Time - O(n)
Space - O(1)
public class Solution {
public boolean hasCycle(ListNode head) {
ListNode slow = head;
ListNode fast = head;
while(fast!=null && fast.next!=null){
slow = slow.next;
fast = fast.next.next;
if(fast==slow) return true;
}
return false;
}
}
