240. Search a 2D Matrix II

Problem

Write an efficient algorithm that searches for a value target in an m x n integer matrix matrix. This matrix has the following properties:

• Integers in each row are sorted in ascending from left to right.

• Integers in each column are sorted in ascending from top to bottom. (link)

Example 1:

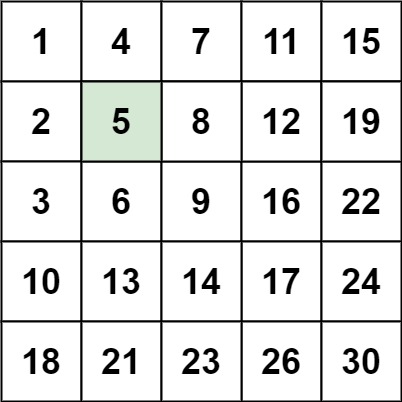
Input: matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
Output: true

Example 2:

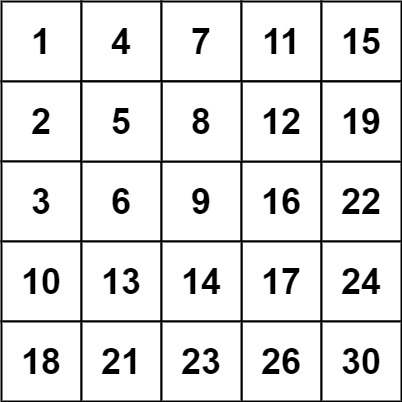
Input: matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20
Output: false

Constraints:

• m == matrix.length

• n == matrix[i].length

• 1 <= n, m <= 300

• -10^9 <= matrix[i][j] <= 10^9

• All the integers in each row are sorted in ascending order.

• All the integers in each column are sorted in ascending order.

• -10^9 <= target <= 10^9

Solution

Optimal Approach

Given that each row and column sorted, we can find the target value by starting from a specific index. The key idea is to move in a direction towards the target value.

The question is, what is that specific index? If we start at (0,0), moving right or down only increases the values, leaving us clueless about the target element's location. The same applies to (m-1,n-1).

However, the position (0,n-1) is interesting. If move down, the values increase, and if we move left, the values decrease. Thus, if we compare the target element with this pivot, we can eliminate one half, giving us the direction in which target element lies.

So if we compare the target element with pivot

• target<pivot: Means it's in the left half i.e., on the row. So, we just move the column left.

• target>pivot: Means it's in the bottom half i.e., on column. So, we just move the row down.

We then compare the new pivot element with the target element and continue to adjust the row and column indices accordingly.

Similarly, the postion (m-1,0) can also be used as the starting element to reach the target element, if present.

Here, we are not using any traditional binary search approach, but the elimination of one half, whether it's a row or column, is similar to binary search.

Time - O(m+n)

Space - O(1)

class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {

        int m = matrix.length;
        int n = matrix[0].length;

        int row = 0;
        int col = n-1;


        while(row<m && col>=0){
            if(matrix[row][col]==target) return true;

            if(matrix[row][col]<target){
                row+=1;
            }
            else{
                col-=1;
            }
        }

        return false;
    }
}