Given an array of integers heights representing the histogram's bar height where the width of each bar is 1, return the area of the largest rectangle in the histogram. (link)
Example 1:
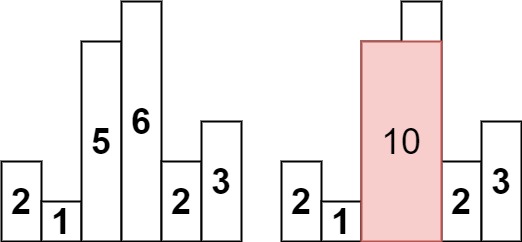
Input: heights = [2,1,5,6,2,3]
Output: 10
Explanation: The above is a histogram where width of each bar is 1.
The largest rectangle is shown in the red area, which has an area = 10 units.
Example 2:
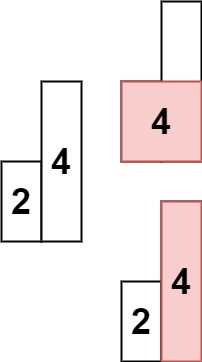
Input: heights = [2,4]
Output: 4
Solution
Brute Force Approach
In order to find the largest rectangle in a histogram, the idea is simple. We consider the current height and calculate how much width it can spread. If the current index height is ‘x’, then we determine how many rectangles on the right and left support this height. From these, we get the width. We calculate the area by multiplying the current height and width. Similarly, we take each element’s height and find out the area. In this way, we take the maximum area from all the areas calculated so far
Time - O(n*n)
Space - O(1)
class Solution {
public int largestRectangleArea(int[] heights) {
int largestArea = 0;
for(int i=0; i<heights.length; i++){
int leftIndex = 0;
for(int j=i-1; j>=0; j--){
if(heights[j]<heights[i]) {
leftIndex = j+1;
break;
}
}
int rightIndex = heights.length-1;
for(int j=i+1; j<heights.length; j++){
if(heights[j]<heights[i]){
rightIndex = j-1;
break;
}
}
int width = rightIndex - leftIndex + 1;
largestArea = Math.max(largestArea, heights[i] * width);
}
return largestArea;
}
}
Better Approach
This approach is built on top of the brute force approach. The idea is the same: with current height, we determine how much width it can spread in the histogram to the left or right. For example, if the height is 5, we can continue to the left if the heights we encounter are greater than or equal to 5. The spread stops if we encounter any height less than 5. The same applies to the right side.
For the current height, we need to find the previous nearest element index(PSE) on the left and also the next nearest element index (NSE) on the right. We can easily calculate the width by using these two indices.
Width = NSE - PSE - 1
We subtract 1 from width to exclude both the NSE and PSE indices since they are not part of the spread.
We already know find out how to find the PSE (or NSE), so we can use that directly.
Time - O(n)
Space - O(n)
class Solution {
public int[] getLeftNse(int[] heights){
int n = heights.length;
int[] leftNse = new int[n];
//Store index, access element using this index
Stack<Integer> stack = new Stack<>();
int usual = -1;
for(int i=0; i<n; i++){
while(!stack.empty() && heights[stack.peek()]>=heights[i]){
stack.pop();
}
leftNse[i] = stack.empty() ? usual : stack.peek();
stack.push(i);
}
return leftNse;
}
public int[] getRightNse(int[] heights){
int n = heights.length;
int[] rightNse = new int[n];
//Store index, access element using this index
Stack<Integer> stack = new Stack<>();
int usual = n;
for(int i=n-1; i>=0; i--){
while(!stack.empty() && heights[stack.peek()]>=heights[i]){
stack.pop();
}
rightNse[i] = stack.empty() ? usual : stack.peek();
stack.push(i);
}
return rightNse;
}
public int largestRectangleArea(int[] heights) {
int n = heights.length;
int[] leftNse = getLeftNse(heights);
int[] rightNse = getRightNse(heights);
int largestArea = 0;
for(int i=0; i<n; i++){
int width = (rightNse[i] - 1) - (leftNse[i] + 1) + 1;
int area = heights[i] * width;
largestArea = Math.max(largestArea,area);
}
return largestArea;
}
}
Optimal Approach
The idea is that we calculate the next smaller element while calculating the previous smaller element. So, when we pop an element from the stack during the PSE (Previous Smaller Element) calculation, it means that for the popped element, the next smaller element will be the current element and the previous smaller element will be the next top element of the stack.
In the stack, instead of storing the elements themselves, we store their indices. We then use these indices to access the elements and perform comparisons.
Time - O(n)
Space - O(n)
class Solution {
public int largestRectangleArea(int[] heights) {
Stack<Integer> stack = new Stack<>();
int maxArea = 0;
for(int i=0; i<heights.length; i++){
while(!stack.empty() && heights[stack.peek()] >= heights[i]){
int currIndex = stack.pop();
int nseIndex = i;
int pseIndex = stack.empty() ? -1 : stack.peek();
maxArea = Math.max(maxArea, heights[currIndex] *(nseIndex-pseIndex-1));
}
stack.push(i);
}
int defaultNseIndex = heights.length;
while(!stack.empty()){
int currIndex = stack.pop();
int pseIndex = stack.empty() ? -1 : stack.peek();
int width = defaultNseIndex - pseIndex - 1;
maxArea = Math.max(maxArea, heights[currIndex] * width);
}
return maxArea;
}
}
