1901. Find a Peak Element II

Problem

A peak element in a 2D grid is an element that is strictly greater than all of its adjacent neighbors to the left, right, top, and bottom.

Given a 0-indexedm x n matrix mat where no two adjacent cells are equal, find any peak element mat[i][j] and return the length 2 array[i,j].

You may assume that the entire matrix is surrounded by an outer perimeter with the value -1 in each cell.

You must write an algorithm that runs in O(m log(n)) or O(n log(m)) time. (link)

Example 1:

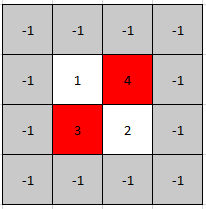
Input: mat = [[1,4],[3,2]]
Output: [0,1]
Explanation: Both 3 and 4 are peak elements so [1,0] and [0,1] are both acceptable answers.

Example 2:

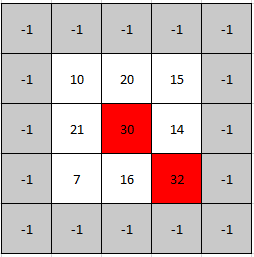
Input: mat = [[10,20,15],[21,30,14],[7,16,32]]
Output: [1,1]
Explanation: Both 30 and 32 are peak elements so [1,1] and [2,2] are both acceptable answers.

Constraints:

• m == mat.length

• n == mat[i].length

• 1 <= m, n <= 500

• 1 <= mat[i][j] <= 10<sup>5</sup>

• No two adjacent cells are equal.

Solution

Optimal Approach - Binary Search

Before diving into this approach, go through the solution for finding a peak in 1D array (link). In the 1D approach, we will determine which half to eliminate and which half of the array might contain the peak.

In the 2D case, we apply a binary search on the row. Based on the mid value, we move into the specific column and find out the index where maximum element present because the maximum element is likely to be one the peaks. We then compare the left and right neighbours around this index and return if it is the peak. Otherwise we have to move left or right based on the following conditions

• Move left: If the left neighbour is greater than the maximum element present in the mid column

• Move right: If the right neighbour is greater than the maximum element present in the mid column.

Reason

• If we move to the greater side because we are moving towards the greatest element of the next half.

Time - O(mlogn)

Space - O(1)

class Solution {
    public int[] findPeakGrid(int[][] mat) {

        int m = mat.length;
        int n = mat[0].length;

        int low = 0;
        int high = n-1;

        while(low<=high){
            int mid = (low+high)/2;

            int maxRowIndex = getMaxOfCol(mat, mid);

            int left = mid-1>=0 ? mat[maxRowIndex][mid-1] : -1;
            int right = mid+1<n ? mat[maxRowIndex][mid+1] : -1;

            int curr = mat[maxRowIndex][mid];

            if(left< curr && curr > right) return new int[]{maxRowIndex, mid};

            if(curr<right){
                low = mid+1;
            } 
            else{
                high = mid-1;
            }
        }
        return new int[]{-1,-1};
    }

    private int getMaxOfCol(int[][] mat, int col){
        int currMax = -1;
        int currMaxIndex = -1;
        for(int i=0; i<mat.length; i++){
            if(currMax<mat[i][col]){
                currMax = mat[i][col];
                currMaxIndex = i;
            }
        }

        return currMaxIndex;
    }
}