4. Median of Two Sorted Arrays

Problem Statement

Given two sorted arrays nums1 and nums2 of size m and n respectively, return the median of the two sorted arrays.

The overall run time complexity should be O(log (m+n)). (link)

Example 1:

Input: nums1 = [1,3], nums2 = [2]
Output: 2.00000
Explanation: merged array = [1,2,3] and median is 2.

Example 2:

Input: nums1 = [1,2], nums2 = [3,4]
Output: 2.50000
Explanation: merged array = [1,2,3,4] and median is (2 + 3) / 2 = 2.5.

Constraints:

nums1.length == m
nums2.length == n
0 <= m <= 1000
0 <= n <= 1000
1 <= m + n <= 2000
-10<sup>6</sup> <= nums1[i], nums2[i] <= 10<sup>6</sup>

Solution

Brute Force Approach (merge sort)

We merge two sorted arrays into a single array and calculate the median of the combined array. The resulting array is sorted.

To merge the arrays, we utilize two pointers pointing to the beginning of the given arrays. A new array is created to store the sorted elements. The core idea of this process involves comparing elements at the i-th and j-th indices of nums1 and nums2. The lesser of the two elements is stored in the new array, and we increment the corresponding index before proceeding further. This method is fundamental to the merge sort algorithm.

Once we obtain the combined sorted array, we directly calculate its median. If the array length is even, the average of the middle two elements is returned. If it is odd, the middle element is returned directly.

Time - O(n1+n2)

Space - O(n1+n2)

class Solution {
    public double findMedianSortedArrays(int[] nums1, int[] nums2) {
        int n1 = nums1.length;
        int n2 = nums2.length;

        int[] arr = new int[n1+n2];

        int i=0, j=0, index = 0;

        while(i<n1 && j<n2){
            if(nums1[i]<=nums2[j]){
                arr[index] = nums1[i];
                index+=1;
                i+=1;
            }else{
                arr[index] = nums2[j];
                index+=1;
                j+=1;
            }
        }

        while(i<n1){
            arr[index] = nums1[i];
            index+=1;
            i+=1;
        }

        while(j<n2){
            arr[index] = nums2[j];
            index+=1;
            j+=1;
        }

        int mid = (n1+n2)/2;
        if((n1+n2)%2==0){
            return (double) (arr[mid-1] + arr[mid])/2;
        }

        return arr[mid];
    }
}

Better Approach (merge sort - no space)

This strategy mirrors the merge sort approach. Unlike traditional methods that require storing all elements, here we only need to store the middle two elements. A counter is employed to determine whether the current element will occupy the middle index. If affirmative, we store it. The counter initiates at 1 and increments with each encountered element in the loop. Subsequently, the median is determined based on whether the array length is even or odd, utilizing the information from the middle two elements.

Time - O(n1+n2)

Space - O(1)

class Solution {
    public double findMedianSortedArrays(int[] nums1, int[] nums2) {
        int n1 = nums1.length;
        int n2 = nums2.length;

        int i=0, j=0, count=1;

        int mid = (n1+n2)/2;

        int x = 0;
        int y = 0;

        while(i<n1 && j<n2){
            int curr = 0;
            if(nums1[i]<=nums2[j]){
                curr = nums1[i];
                i+=1;
            }
            else{
                curr = nums2[j];
                j+=1;
            }

            if(count==mid) x = curr;
            if(count==mid+1) y = curr;

            count+=1;
        }

        while(i<n1){

            if(count==mid) x = nums1[i];
            if(count==mid+1) y = nums1[i];
            i+=1;

            count+=1;
        }

        while(j<n2){

            if(count==mid) x = nums2[j];
            if(count==mid+1) y = nums2[j];
            j+=1;

            count+=1;
        }

        if((n1+n2)%2==0) return (x+y)/2.0;
        return y;
    }
}

Optimal Approach - Binary Search

Given that the two arrays are sorted, employing binary search is feasible. However, applying binary search in this scenario can be challenging, as it is commonly used on a single array or within a range of answers. In this case, binary search is applied to the range of potential answers. Determining the answer range for the given arrays is difficult, and to validate the median, one would need to traverse the combined array up to the midpoint. To address this, the symmetry property is utilized.

Valid Symmetry - Consider a scenario where there are two arrays, and the goal is to find the median of the combined array. By aligning the two arrays side by side, it becomes evident that having 5 elements on each side is essential. The focus is on the left side of these 5 elements. Various combinations of elements from arr1 and arr2 can form these 5 elements. The selection of elements from arr1, ranging from all elements (up to a maximum of 5) to none, influences the elements chosen from arr2 in the left half.

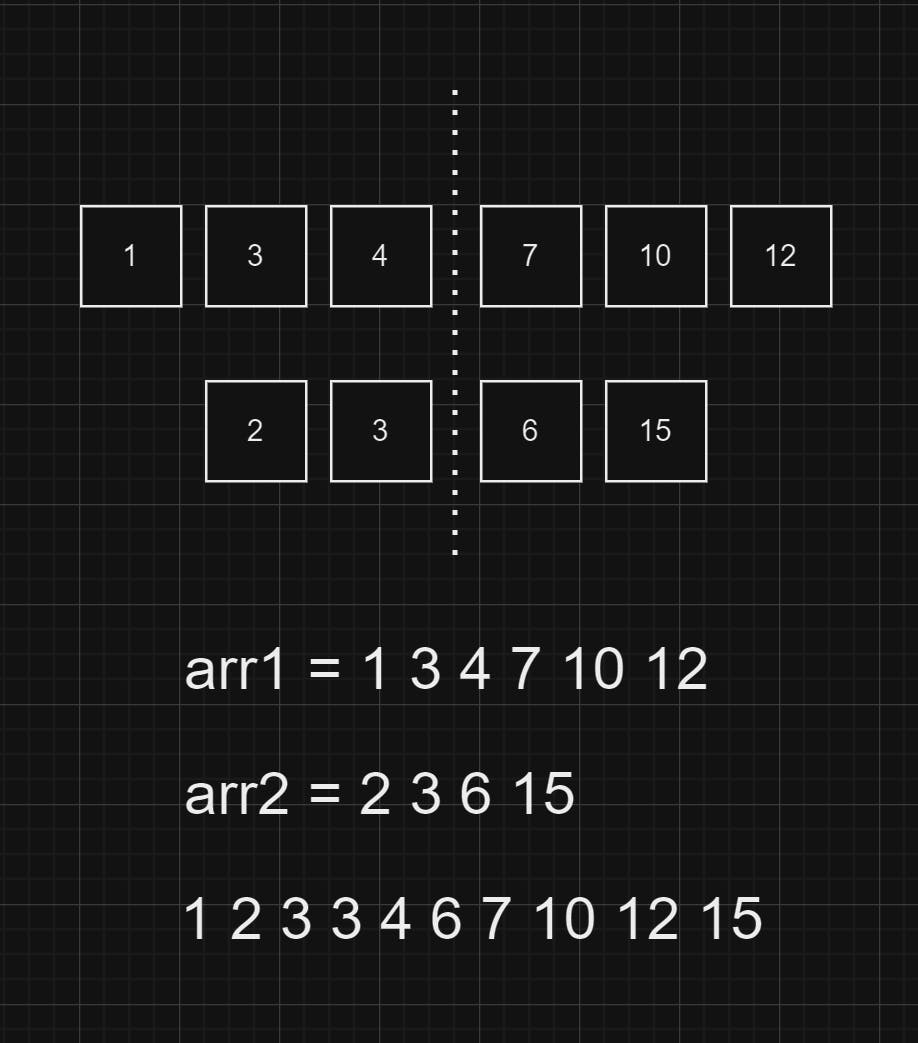
Answer Range - Binary search is applied to determine the number of elements that will be selected from array 1, forming a sorted array. The answer range is defined as [0, the length of arr1].

Binary Search Conditions - The objective is to identify or approach the number of elements on the left side to ensure array sorting.

Calculation Steps:

Compute the midpoint within the answer range and obtain the values of (l1, r1) and (l2, r2).
- l1 = arr1[mid - 1], r1 = arr1[mid]
- l2 = arr2[leftover - 1], r2 = arr2[leftover]
- leftover = (total number of elements on the left) - mid (elements of arr1 on the left)
mid1 corresponds to mid, and mid2 corresponds to leftover. (Code)

Conditions:

Base condition for a sorted array: l1 < r2 and l2 < r1
If l1 > r2, move high = mid - 1 to decrease the value of l1 and meet the base condition.
If l2 > r1, move low = mid + 1 to increase the value of r1 and meet the base condition.

Once the base condition is met, halt the process and return the answer. The median is then calculated based on (l1, r1) and (l2, r2).

Median Calculation:

For an even total (n1 + n2), median = [Max(l1, l2) + Min(r1, r2)] / 2
For an odd total, median = Max(l1, l2)

In the odd scenario, the middle element is placed on the left side, accommodating one extra element on the left (e.g., total length 5 results in 3 on the left and 2 on the right). To calculate the midpoint, 1 is added to the sum, ensuring an extra element on the left for odd cases. The floor function is applied for both odd and even sums.

Code

Time - O(min(logn1, logn2)