74. Search a 2D Matrix

Problem

You are given an m x n integer matrix matrix with the following two properties:

• Each row is sorted in non-decreasing order.

• The first integer of each row is greater than the last integer of the previous row.

Given an integer target, return true if targetis in matrix or false otherwise.

You must write a solution in O(log(m * n)) time complexity. (link)

Example 1:

Input: matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
Output: true

Example 2:

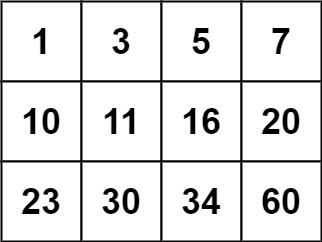
Input: matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13
Output: false

Constraints:

• m == matrix.length

• n == matrix[i].length

• 1 <= m, n <= 100

• -10<sup>4</sup> <= matrix[i][j], target <= 10<sup>4</sup>

Solution

Optimal Approach - Binary Search

This approach is similar to performing a binary search for a target in a one-dimensional array. The only difference is that we keep low at 0 and high at m*n. The idea is to number all the elements in a flat manner, without using the second dimension. Here, we convert any number x into its corresponding i and j coordinates.

• Row number i = x / (length of each row): We divide x by length of each row because it gives the number of rows x spans.

• Column number j = x % (length of each row): By finding out the remainder, we get the position of the element from the start of the row. This is because, after accounting for the complete rows, the remainder represents the number of elements left in the current row.

class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        int m = matrix.length;
        int n = matrix[0].length;

        int low = 0;
        int high = m*n-1;

        while(low<=high){
            int mid = (low+high)/2;

            int i = mid/n;
            int j = mid%n;

            if(matrix[i][j]==target) return true;

            if(matrix[i][j]<target){
                low = mid +1;
            }
            else{
                high = mid -1;
            }
        }
        return false;
    }
}