Introduction

• Arrays and linked lists are flat structures, whereas a tree is a hierarchical structure.

• If a tree has only 2 children, then it is called a binary tree.

Terminology

• Root: The head of the tree is called the root node.

• Leaf node: A node that doesn’t have any children.

• Subtree: If we pick any node, we can consider it as a root node for its children, grandchildren, and so on. This subpart is called a subtree.

• Ancestors: All the nodes that are above the root parent node are called the ancestors of the current node.

Types of Binary Tree

There are 5 types of binary tree

1. Full Binary tree

Either has 0 or 2 children.

2. Complete Binary tree

• All the levels are filled except the last level.

• The last level has all nodes as left as possible.

3. Perfect Binary Tree

All leaf nodes are at the same level.

4. Balanced Binary Tree

Height of tree at maximum can be log(N) base2. Where N is number of nodes in the tree.

5. Degenerate Tree

Every node has single child.

Application 1

Problem

Given an integer i. Print the maximum number of nodes on level i of a binary tree. (link)

Example 1:

Input: 5
Output: 16

Example 2:

Input: 1
Output: 1

Solution

class Solution {
    static int countNodes(int i) {
        return (int)Math.pow(2,i-1);
    }
}

Binary Tree Representation

Code 1

class Node{
    int data;

    Node left;

    Node right;

    public Node(int data){

        this.data = data;
    }
}

Code 2 (Leetcode version)

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */

Problem

You are given an array nodes. It contains 7 integers, which represents the value of nodes of the binary tree in level order traversal. You are also given a root of the tree which has a value equal to nodes[0].

Your task to construct a binary tree by creating nodes for the remaining 6 nodes.

Example:

Input: 
nodes = [1 2 3 4 5 6 7]
Output: 
         1
       /   \
     2       3
   /  \     /  \
   4  5    6   7
Explanation: 
The 7 node binary tree is represented above.

Constraints:

vec.length = 7

1<=vec[i]<=100

Solution

Approach 1 (For 7 nodes)

class Solution{

    public static void createTree(Node root0, ArrayList<Integer> v ){

        Node node2 = new Node(v.get(1));
        Node node3 = new Node(v.get(2));
        Node node4 = new Node(v.get(3));
        Node node5 = new Node(v.get(4));
        Node node6 = new Node(v.get(5));
        Node node7 = new Node(v.get(6));

        root0.left = node2;
        root0.right = node3;

        node2.left = node4;
        node2.right = node5;


        node3.left = node6;
        node3.right = node7;
    }
}

Approach 2 (For n nodes)

class Solution{

    private static void createSubTree(Node temp, ArrayList<Integer> v, int index){
        if(index>=v.size()) return;
        int leftIndex = 2*index+1;
        int rightIndex = 2*index+2;
        if(leftIndex<v.size()) {
            temp.left = new Node(v.get(leftIndex));
            createSubTree(temp.left, v, leftIndex);
        }
        if(rightIndex<v.size()) {
            temp.right = new Node(v.get(rightIndex));
            createSubTree(temp.right, v, rightIndex);
        }

    }
    public static void createTree(Node root0, ArrayList<Integer> v ){
        // Code here
        createSubTree(root0, v, 0);
    }
}

Traversals

There are 2 types of traversals

• DFS - Depth First Search

• BFS - Breadth First Search

DFS

There are 3 types of DFS traversals

• Inorder traversal (Root in between Left and Right)

• Pre-order traversal (Root before Left and right)

• Post-order traversal (Root after Left and right)

Inorder traversal (Left-Root-Right)

Problem

Given the root of a binary tree, return the inorder traversal of its nodes' values.(link)

Example 1:

Input: root = [1,null,2,3]

Output: [1,3,2]

Solution

class Solution {
    private void inorder(TreeNode root, List<Integer> ans){
        if(root==null) return;

        inorder(root.left,ans);
        ans.add(root.val);
        inorder(root.right,ans);
    }
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> ans = new ArrayList<>();
        inorder(root,ans);
        return ans;
    }
}

Pre-order traversal (Root-Left-Right)

Problem

Given the root of a binary tree, return the preorder traversal of its nodes' values. (link)

Example 1:

Input: root = [1,null,2,3]

Output: [1,2,3]

Solution

class Solution {
    private void preorder(TreeNode root, List<Integer> ans){
        if(root==null) return;

        ans.add(root.val);
        preorder(root.left,ans);
        preorder(root.right,ans);
    }

    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> ans = new ArrayList<>();
        preorder(root,ans);
        return ans;
    }
}

Post-order traversal (Left-Right-Root)

Problem

Given the root of a binary tree, return the postorder traversal of its nodes' values. (link)

Example 1:

Input: root = [1,null,2,3]

Output: [3,2,1]

Solution

class Solution {
    private void postorder(TreeNode root, List<Integer> ans){
        if(root==null) return;

        postorder(root.left,ans);
        postorder(root.right,ans);
        ans.add(root.val);
    }
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> ans = new ArrayList<>();
        postorder(root,ans);
        return ans;
    }
}

Time and Space Complexties

Time - O(n)

Space - O(n) Auxilary stack space

If the tree has n nodes, then our code has to go through all the nodes, hence the time complexity is O(n).

For space, if the tree is a degenerate binary tree, then all the nodes are attached just like a linked list (single path), hence O(n) for auxiliary space. Or we can say the space is length of the maximum path in the tree.

BFS - Breadth Fast Search

BFS is a level order traversal. It traveses the binary tree level-wise.

Problem

Given the root of a binary tree, return the level order traversal of its nodes' values. (i.e., from left to right, level by level). (link)

Example 1:

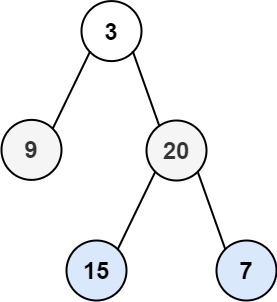
Input: root = [3,9,20,null,null,15,7]
Output: [[3],[9,20],[15,7]]

Solution

The main idea in BFS is to store the current level nodes in the queue, pop each one from the front, and add all its children to the end of the queue. We continue this process of popping and adding children until the level size is reached. After that, the nodes in the queue move to the next level iteration. When we pop the nodes, we also store the elements in the current level list. Once the level size is finished, we add the current level elements list to the all-level list array, which stores all the level lists.

class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {

        List<List<Integer>> ans = new ArrayList<>();

        if(root==null) return ans;

        Queue<TreeNode> queue = new ArrayDeque<>();
        queue.add(root);

        while(!queue.isEmpty()){
            List<Integer> level = new ArrayList<>();
            int size = queue.size();

            for(int i=0; i<size; i++){
                TreeNode currNode = queue.poll();
                level.add(currNode.val);
                if(currNode.left!=null) queue.add(currNode.left);
                if(currNode.right!=null) queue.add(currNode.right);
            }
            ans.add(level);
        }

        return ans;
    }
}

Time and Space Complexity

Time - O(n)

Space - O(n/2)

Since there are ( n ) nodes, visiting each node indicates a time complexity of ( O(n) ).

For space complexity:

• O(1) for a degenerate binary tree.

• O(n/2) for a complete binary tree with the last level completely filled.