Height of a Binary Tree - Max Depth

Problem

Given the root of a binary tree, return its maximum depth.

A binary tree's maximum depth is the number of nodes along the longest path from the root node down to the farthest leaf node. (link)

Example 1:

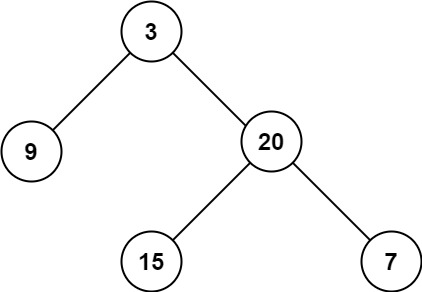
Input: root = [3,9,20,null,null,15,7]
Output: 3

Example 2:

Input: root = [1,null,2]
Output: 2

Solution

We prefer Depth-First Search (DFS) over Breadth-First Search (BFS) for calculating the height of a binary tree, even though both have a time complexity of O(n). This preference is due to the following reasons:

1. Space Complexity: While both DFS and BFS have a worst-case space complexity of O(n), this scenario occurs only in degenerate or skewed trees, which are rare.

2. Average Case: In most cases, binary trees are balanced, and the average height is O(log n). Therefore, DFS typically requires O(log n) space, which is more efficient than BFS.

Recursive Approach (DFS)

To determine the maximum depth of a binary tree, follow these steps:

1. Calculate the height of the left subtree.

2. Calculate the height of the right subtree.

3. Identify the greater height between the two.

4. Add 1 to this maximum height to account for the root node.

Thus, the formula for the height of the tree is:

height=max(left height,right height)+1

This ensures that the root node is included in the total height calculation.

Complexity

• Time Complexity: (O(n)) - where (n) is the total number of nodes.

• Space Complexity: (O(n)) - Auxiliary space required for a degenerate binary tree.

class Solution {
    public int maxDepth(TreeNode root) {
        if(root==null) return 0;

        int leftDepth = maxDepth(root.left);
        int rightDepth = maxDepth(root.right);

        return Math.max(leftDepth, rightDepth)+1;
    }
}

Iterative Approach (BFS)

The height of a binary tree is defined as the total number of levels it contains. To determine this, we can use Breadth-First Search (BFS), which processes the tree level by level.x

1. Use BFS: Traverse the tree level by level.

2. Count the Levels: Each level processed by BFS corresponds to one level in the tree.

Time - O(n)

Space - O(n) (Last level has n/2 nodes maximum, queue space)

class Solution {
    public int maxDepth(TreeNode root) {
        if(root==null) return 0;

        Queue<TreeNode> queue = new ArrayDeque<>();

        queue.add(root);

        int level = 0;

        while(!queue.isEmpty()){

            level+=1;

            int size = queue.size();

            for(int i=0; i<size; i++){
                TreeNode temp = queue.poll();
                if(temp.left!=null) queue.add(temp.left);
                if(temp.right!=null) queue.add(temp.right);
            }
        }

        return level;
    }
}