Here we illustrates the implementation of DFS iteratively using stacks. For the recursive implementation of DFS refere this article.
Preorder Traversal
Problem
Given the root of a binary tree, return the preorder traversal of its nodes' values. (link)
Example 1:
Input: root = [1,null,2,3]
Output: [1,2,3]
Explanation:
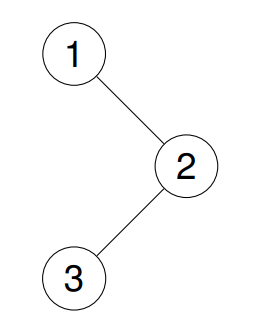
Example 2:
Input: root = [1,2,3,4,5,null,8,null,null,6,7,9]
Output: [1,2,4,5,6,7,3,8,9]
Explanation:
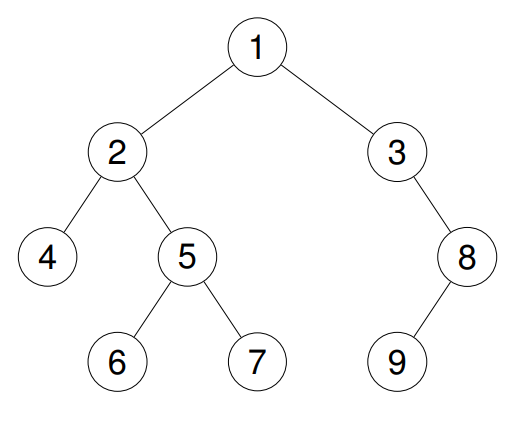
Example 3:
Input: root = []
Output: []
Example 4:
Input: root = [1]
Output: [1]
Solution
First, push the root node into the stack and start the iteration for the pre-order traversal. We pop out the top element of the stack and push the left and right children into the stack. We first insert the right child, then the left child, because when we pop out the first element, we get the left child.
Whenever we pop out, we store that element's value into the pre-order answer list.
Time - O(n)
Space - O(n)
class Solution {
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> ans = new ArrayList<>();
if(root==null) return ans;
Stack<TreeNode> stack = new Stack<>();
stack.push(root);
while(!stack.isEmpty()){
TreeNode currNode = stack.pop();
ans.add(currNode.val);
if(currNode.right!=null) stack.push(currNode.right);
if(currNode.left!=null) stack.push(currNode.left);
}
return ans;
}
}
Inorder Traversal
Problem
Given the root of a binary tree, return the inorder traversal of its nodes' values.(link)
Example 1:
Input: root = [1,null,2,3]
Output: [1,3,2]
Explanation:

Example 2:
Input: root = [1,2,3,4,5,null,8,null,null,6,7,9]
Output: [4,2,6,5,7,1,3,9,8]
Explanation:

Example 3:
Input: root = []
Output: []
Example 4:
Input: root = [1]
Output: [1]
Solution
The main idea is to traverse to the left side of the tree, pushing each encountered node onto the stack. When we reach a node with a null, we pop the top of the stack, add its value to the in-order answer list, and then shift our traversal to the right. We repeat this process: moving left until we reach a null, then shifting to the right.
Note that whenever we pop a node, we store its value in our in-order list and push the current node onto the stack, regardless of whether it has a left or right child.
This approach ensures that we visit the left child first, then pop the root, and finally traverse to the right.
Time - O(2*n)
Space - O(n)
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> ans = new ArrayList<>();
if(root==null) return ans;
Stack<TreeNode> stack = new Stack<>();
stack.push(root);
TreeNode currNode = root;
while(!stack.isEmpty()){
if(currNode!=null){
currNode = currNode.left;
}
else{
currNode = stack.pop();
ans.add(currNode.val);
currNode = currNode.right;
}
if(currNode!=null) stack.push(currNode);
}
return ans;
}
}
Postorder Traversal
Problem
Given the root of a binary tree, return the postorder traversal of its nodes' values.(link)
Example 1:
Input: root = [1,null,2,3]
Output: [3,2,1]
Explanation:

Example 2:
Input: root = [1,2,3,4,5,null,8,null,null,6,7,9]
Output: [4,6,7,5,2,9,8,3,1]
Explanation:

Example 3:
Input: root = []
Output: []
Example 4:
Input: root = [1]
Output: [1]
Solution - 2 stacks
We use two stacks: one for operations and another for storing the post-order traversal result.
Initially, we store the root in the first stack and begin the iteration. During each iteration, we pop the top element from the first stack, push its left and right children (if they are not null) into the stack, and then push the popped element into the second stack. This process continues until the first stack is empty.
Once the first stack is empty, we pop elements from the second stack and store them in the post-order traversal list.
Time - O(2*n)
Space - O(2*n)
class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> ans = new ArrayList<>();
if(root==null) return ans;
Stack<TreeNode> stack1 = new Stack<>();
Stack<TreeNode> stack2 = new Stack<>();
stack1.push(root);
while(!stack1.isEmpty()){
TreeNode currNode = stack1.pop();
if(currNode.left!=null) stack1.push(currNode.left);
if(currNode.right!=null) stack1.push(currNode.right);
stack2.push(currNode);
}
while(!stack2.isEmpty()){
ans.add(stack2.pop().val);
}
return ans;
}
}
Solution - 1 stack
Use one stack and a current node to traverse each node. Initially, the current node points to the root node and starts the iteration. Move the current node to the left until reaching a null node. When a null node is reached, check the top element of the stack, move the current node to its right, and continue moving left. If the right node is also null, pop the top element and store the value in the post-order answer array. Then, take the same popped element and check if it is the right child of the top element of the stack. If it is, pop the top element and add it to the answer list. This process continues. The reason is that when the right pointer is null, it indicates a leaf node or left part is done. After this, check if the leaf node is the right child of the top element of the stack, which might be the parent of the leaf node, and add it to the answer list.
Time - O(2*n)
Space - O(n)
class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> ans = new ArrayList<>();
if(root==null) return ans;
Stack<TreeNode> stack = new Stack<>();
TreeNode curr = root;
while(!stack.isEmpty() || curr!=null){
if(curr!=null){
stack.push(curr);
curr = curr.left;
}
else{
TreeNode temp = stack.peek().right;
if(temp==null){
TreeNode top = stack.pop();
ans.add(top.val);
while(!stack.isEmpty() && stack.peek().right == top){
top = stack.pop();
ans.add(top.val);
}
}
else{
curr = temp;
}
}
}
return ans;
}
}
3 traversals using one stack
Problem
You have been given a Binary Tree of 'N' nodes, where the nodes have integer values.
Your task is to return the ln-Order, Pre-Order, and Post-Order traversals of the given binary tree. (link)
For example : For the given binary tree:
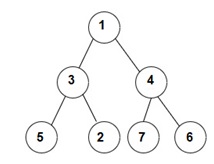
The Inorder traversal will be [5, 3, 2, 1, 7, 4, 6].
The Preorder traversal will be [1, 3, 5, 2, 4, 7, 6].
The Postorder traversal will be [5, 2, 3, 7, 6, 4, 1].
Detailed explanation ( Input/output format, Notes, Images )
Sample Input 1 :
1 2 3 -1 -1 -1 6 -1 -1
Sample Output 1 :
2 1 3 6
1 2 3 6
2 6 3 1
Explanation of Sample Output 1 : The given binary tree is shown below:

Inorder traversal of given tree = [2, 1, 3, 6]
Preorder traversal of given tree = [1, 2, 3, 6]
Postorder traversal of given tree = [2, 6, 3, 1]
Sample Input 2 :
1 2 4 5 3 -1 -1 -1 -1 -1 -1
Sample Output 2 :
5 2 3 1 4
1 2 5 3 4
5 3 2 4 1
Explanation of Sample Output 2 :
The given binary tree is shown below:

Inorder traversal of given tree = [5, 2, 3, 1, 4]
Preorder traversal of given tree = [1, 2, 5, 3, 4]
Postorder traversal of given tree = [5, 3, 2, 4, 1]
Solution
We use a stack to store pairs containing a tree node and its current status, which can be 1, 2, or 3. If the status is 1, the node is added to the preorder list; if 2, to the in-order list; and if 3, to the post-order list.
Initially, the stack starts with the root node having a status of 1. During each iteration, we peek at the stack to get the node and its status. If the status is 1, we increment it to 2 and push the left child onto the stack. If the status is 2, we increment it to 3 and push the right child onto the stack. If the status is 3, we pop the top element from the stack. Each time we change the status in the if-else blocks, we add the node's value to the respective order list. We only pop the top element when the status is 3.
This status concept works because it ensures the root is first added to the preorder list, then to the in-order list, and finally to the post-order list.
Note: A custom Pair class was used. Note that this Pair class cannot be public within the same file as the pubic Solution class, so it uses the default access modifier.
Time - O(3*n) + O(n) for stack iteration
Space - O(n)
public class Solution {
public static List<List<Integer>> getTreeTraversal(TreeNode root) {
List<List<Integer>> ans = new ArrayList<>();
List<Integer> preorder = new ArrayList<>();
List<Integer> inorder = new ArrayList<>();
List<Integer> postorder = new ArrayList<>();
ans.add(inorder);
ans.add(preorder);
ans.add(postorder);
Stack<Pair<TreeNode, Integer>> stack = new Stack<>();
stack.push(new Pair(root, 1));
while(!stack.isEmpty()){
Pair<TreeNode, Integer> top = stack.peek();
TreeNode node = top.getKey();
if(top.getValue()==1){
top.setValue(2);
preorder.add(node.data);
if(node.left!=null) stack.push(new Pair<>(node.left, 1));
}
else if(top.getValue()==2){
top.setValue(3);
inorder.add(node.data);
if(node.right!=null) stack.push(new Pair<>(node.right, 1));
}
else{
postorder.add(node.data);
stack.pop();
}
}
return ans;
}
}
Custome Pair Class
class Pair<K,V>{
private K key;
private V value;
public Pair(K key, V value){
this.key = key;
this.value = value;
}
public K getKey(){
return key;
}
public V getValue(){
return value;
}
public void setKey(K key){
this.key = key;
}
public void setValue(V value){
this.value = value;
}
}
